Thanks to my INSEAD friend Sergio Werner for pointing me to a new source of puzzles and science articles – http://www.quantamagazine.org. I am reproducing a puzzle posted there by Pradeep Mutalik.
Neural networks and deep learning are the buzzwords of the day. Here is a puzzle that shows the basic mechanics of a neural network.
We’re going to create a simple network that converts binary numbers to decimal numbers. Imagine a network with just two layers — an input layer consisting of three units and an output layer with seven units. Each unit in the first layer connects to each unit in the second, as shown in the figure below.
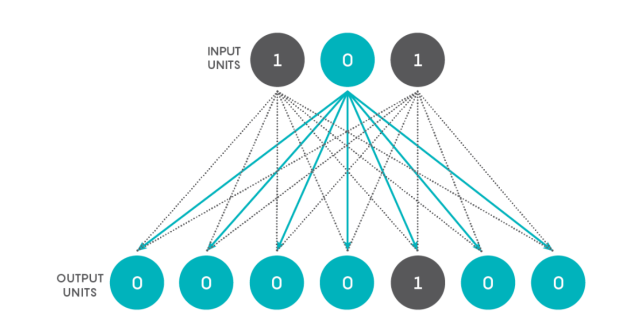
As you can see, there are 21 connections. Every unit in the input layer, at a given point in time, is either off or on, having a value of 0 or 1. Every connection from the input layer to the output layer has an associated weight that, in artificial neural networks, is a real number between 0 and 1. Just to be contrary, and to make the network a touch more similar to an actual neural network, let us allow the weight to be a real number between –1 and 1 (the negative sign signifying an inhibitory neuron). The product of the input’s value and the connection’s weight is conveyed to an output unit as shown below. The output unit adds up all the numbers it gets from its connections to obtain a single number, as shown in the figure below using arbitrary input values and connection weights for a single output unit. Based on this number, the output number decides what its state is going to be. If it is more than a certain threshold, the unit’s value becomes 1, and if not, then its value becomes 0. We can call a unit that has a value of 1 a “firing” or “activated” unit and a unit with a value of 0 a “quiescent” unit.

Figure 2: Puzzle #198
Our three input units from top to bottom can have the values 001, 010, 011, 100, 101, 110 or 111, which readers may recognize as the binary numbers from 1 through 7.
Now the question: Is it possible to adjust the connection weights and the thresholds of the seven output units such that every binary number input results in the firing of only one appropriate output unit, with all the others being quiescent? The position of the activated output unit should reflect the binary input value. Thus, if the original input is 001, the leftmost output unit (or bottommost when viewed on a phone, as shown in the top figure) alone should fire, whereas if the original input is 101, the output unit that is fifth from the left (or from the bottom on a phone) alone should fire, and so on.
If you think the above result is not possible, try to adjust the weights to get as close as you can. Can you think of a simple adjustment, using additional connections but not additional units, that can improve your answer?
As always, please send your answers as comments within the blog (preferred), or send an e-mail to alokgoyal_2001@yahoo.com. Please do share the puzzle with others if you like, and please also send puzzles that you have come across that you think I can share in this blog.
Happy neuron-firing over the weekend!