This is a beautiful puzzle contributed by Suman Saraf – thanks Suman!
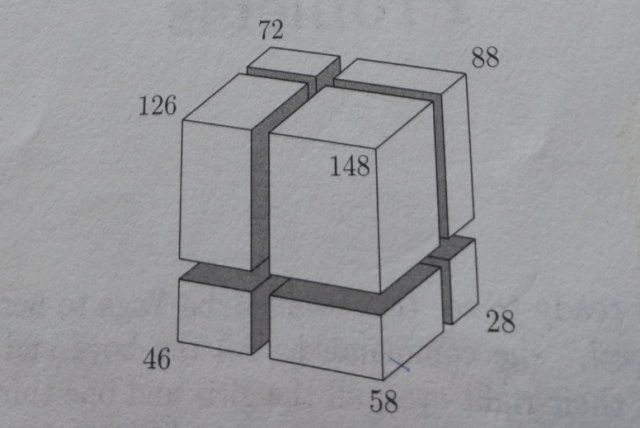
A wooden block is divided into eight smaller blocks by the three cuts, as shown in the figure. The areas of the seven visible blocks are labeled. What is the area of the 8th block?
As always, please send your answers as comments within the blog (preferred), or send an e-mail to alokgoyal_2001@yahoo.com. Please do share the puzzle with others if you like, and please also send puzzles that you have come across that you think I can share in this blog.
Happy blocking and tackling!

Sum of areas of one set of non-adjacent blocks will be equal to the areas of the other set of non-adjacent blocks.
(72+148+46+28)=(126+88+58+X)
X=22
I have done this puzzle before.
Observe that the sum of the surface areas of one set of mini cuboids which do not share a face but share an edge at least one of the others will equal the sum of the areas of the other set. Let A be the area of the 8th block.
We get 88+58+126+A=148+28+46+72.
This gives A=22.
Clearly the area of hidden block is 22