This was a beautiful puzzle and amongst my favourite geometry puzzles. Unfortunately I did not get a perfect answer from anyone, even though I did receive an answer from Abhinav Jain and Pratik Poddar. I am taking the liberty of reproducing the answer from the book “Problem Solving Strategies in Mathematics”, which is where this puzzle was taken from.

Please look at the figure below:

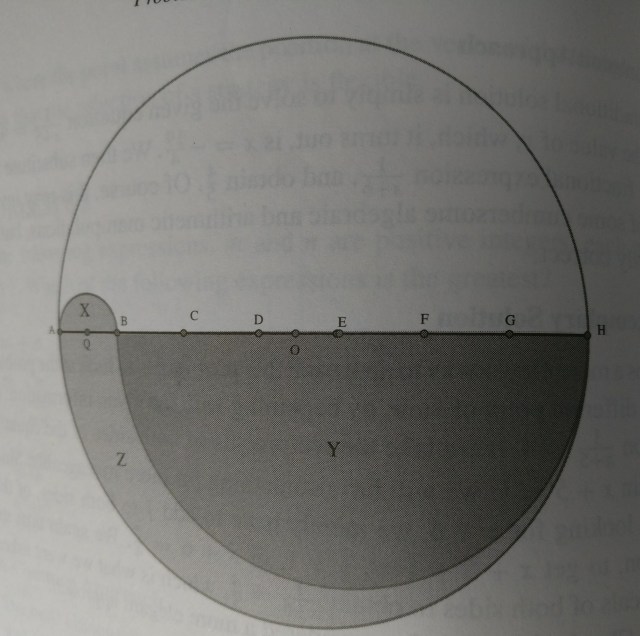
Solution to Puzzle #173

Typical solution to this puzzle is to draw concentric circles, but the exact radii of these circles is very hard to measure.

Instead we begin with our given circle and mark off a length along the diameter which is one-seventh of the distance from one endpoint as shown in the figure above. Please look at the area Z+X. Notice that the diameters of X, Y and the original semi-circle are in the ratio of 1:6:7, and therefore their areas are in the ratio of 1:36:49.

Please note that Z happens to be Area of the original semi-circle minus area of Y, and therefore ratio of Z to the original semicircle is (49-36):49 or 13:49, and therefore ratio of Z+X to the original circle is (13+1):49, which is 2:7, and if we therefore extrapolate, the ratio of (Z+X) to the original circle is 1:7, so we have been able to divide the original circle into a 1/7th part.

We can similarly draw semicircles with diameters AC, AD, AE, AF, AG and AH, which when taken together partition the circle into seven parts.

Hope you all enjoyed the puzzle.